経時測定データ（単に、経時データと呼ぶ）は、複数の対象者についてある反応変数（結果変数）を時間経過とともに、あるいは、異なった条件のもとで、繰り返し測定して得られたデータのことです。具体的なデータ例と分析趣旨を下記に数例挙げておきます。
　講義時間　10:00〜18:00

昨年までは、2日間で開催していた講義ですが、藤越康祝先生に無理を言って１日の講座になるように検討をお願いしました。下記の講座内容は、多少の変更があることと思います。
経時データは、臨床試験データや成長データなど、数多くみられます。例えば、ヒトの降圧剤の効果を調べるために、投与後に複数の時点で測定される血圧の測定値、少年の顎の骨の成長を調べるために、８歳から１４歳まで２年ごとに測定した下顎枝の長さ、などが典型的な経時データです。対象者は個人である必要はなく、地域、事業所などでもよく、また、計量経済分野における経時データはパネルデータと呼ばれます。

そこで得られる経時データから、次のような問題を明らかにすることに関心があります。

[1] 個体が時間とともにどのように変化するか。 [2] 個体間の変化の違い、あるいは、個体がいくつかの 　　グループに分かれているとき 　　グループ間の変化の違いは何か。 [3] 変化を特徴づけ、予測したい。

本講義では、このような問題に対して代表的な統計的モデリングとその分析法について、実際の経時データをもとに解説し、討議します。混合効果分散分析モデルや多変量アプローチは、すべての個体に対して、同じ時点あるいは条件で測定されたバランスド経時データに対して適用される方法です。これに対して、線形混合モデルはアンバランスド経時データに対しても適用されます。

講師は、広島大学名誉教授・藤越康祝先生（上記写真、世界で秀でた統計学者の５人に入る先生で、とても優しい先生です）、実際のデータによる演習(デモ)を諏訪東京理科大学の櫻井哲郎先生が行います。難しいことでも分かり易く話すことのできる若い先生です。藤越康祝先生は、そこで使う方法論の基本的な考え方を丁寧に話し、それを「R」を使って実例で櫻井先生がデモを行います。この実際のデータによる演習が５割とお考え下さい。そこで用いたプログラムは差し上げています。
統計データ分析の中で、この科目や、分散分析法を「特論」として、上級講座と統計科学研究所では呼んでいますが、難易度は「統計データ分析�T」ほど難しくはありません。講座の開催は、１年に一回を目標に開催しています。

学習支援のため、講義のパワーポイントと関連資料をUSBを通して提供しています。当日パソコンを持参しない方はUSBをご持参下さい。

講座内容
（１） 経時データとは。
　　（例）医薬データ、成長データ、経済データ、教育データ、社会データ、
　　　　　などにおける経時データ
（２）混合効果分散分析モデル；分散分析法、共分散構造の検証、多重比較法
　　（例）降圧剤投与による血圧の経時的変化
（３）多変量アプローチ；成長曲線（多変量分散分析）モデル分析、
　　　　　　　　　　　　プロファイル分析。
　　（例）顎の成長データ分析、犬のカリュム血中濃度の経時的変化分析、
　　　　　教育データのプロファイル分析
（４）線形混合モデル；線形回帰モデル、単純な線形混合モデル、
　　　　　　　　　　　ランダム係数モデル。　　
　　（例）経口ブドウ糖負荷試験データの分析、透析患者の限界ろ過圧力と
　　　　　限界ろ過率との関係、
（５）パネルデータ分析；経時モデルのパネルデータへの応用、
　　　　　　　　　　　　動学的パネルデータモデル。
　　（例）家計における所得変動の要因分析、企業の年間利益分析
（６）経時データモデルの選択；線形回帰モデルか線形混合モデルか、
　　　　　　　　　　　　　　　モデルの比較、AIC規準。
　　（例）顎の骨の成長は１次式か２次式か、
（７）その他の話題；　離散経時データ分析、欠側がある場合の分析法。
　　（例）大気汚染データ（子供の喘息は母親の喫煙と関係があるか）
（８）質疑応答


経時データ解析の具体的なデータ例と分析趣旨

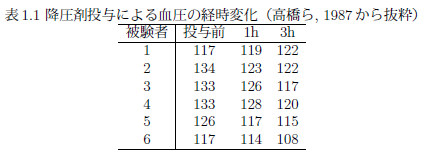
（１） 降圧剤投与による血圧の経時変化データ
混合効果分散分析法を用いて、個体間の違いを考慮しながら、血圧の変化が有意なものであるかを調べる。また、降圧剤投与群と同じ時点で測定された対照群のデータを用いて、両群の変化に有意の違いがあるかどうかを調べる。

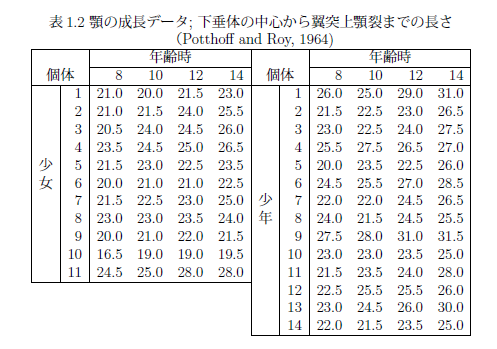
（２） 顎の成長データ
測定値が年齢の１次式で表されるか、あるいは、２次式で表されるかに関心があり、二つのモデルを想定して分析する。一つは、成長曲線モデル（一般化多変量分散分析法）で、他は線形混合モデルである。さらに、どのモデルが適切であるかについて、モデル選択規準を用いて考察する。

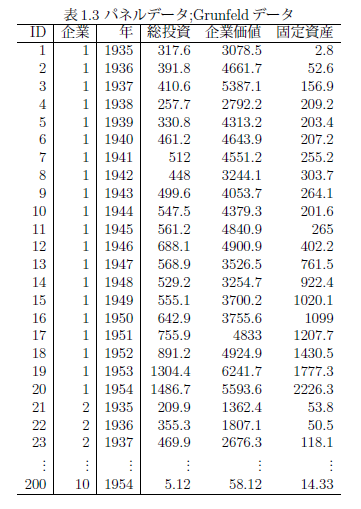
（３） Grunfeldデータ
アメリカの有名な企業１０社の２０年間に渡るデータを基にして、総投資を企業価値と有形固定資産から予測する問題を考える。そのため、固定効果モデルと変量効果モデルを想定した予測法を示す。

（4）数学の問題１,2,3,4を解くのにかかった時間

	被実験者	1	2	3	4
G1	1	43	90	51	67
	2	87	36	12	14
	3	18	56	22	68
	4	34	73	34	87
	5	81	55	29	54
	6	45	58	62	44
	7	16	35	71	37
	8	43	47	87	27
	9	22	91	37	78
平均		43.222	60.111	45.000	52.889
G2	1	10	81	43	33
	2	58	84	35	43
	3	26	49	55	84
	4	18	30	49	44
	5	13	14	25	45
	6	12	8	40	48
	7	9	55	10	30
	8	31	45	9	66
平均		22.125	45.750	33.250	49.125